Utiliser la loi normale
Statistiques descriptives
 La statistique - Enjeux
La statistique - Enjeux
 Démarche statistique
Démarche statistique
 Les variables
Les variables
 Les tableaux
Les tableaux
 Les graphiques
Les graphiques
 Parametres statistiques
Parametres statistiques
Distributions statistique
 Probabilite
Probabilite
 Distribution statistiques
Distribution statistiques
 Distribution normale
Distribution normale
 Distribution binomiale
Distribution binomiale
 Distribution de Poisson
Distribution de Poisson
 Courbe de Gauss avec Excel
Courbe de Gauss avec Excel
 Echantillonnage
Echantillonnage
 Estimation de paramètres
Estimation de paramètres
 Théorème central limite
Théorème central limite
 Tests statistiques
Tests statistiques
Ce que vous allez apprendre sur cette page
- Interpréter une loi normale
- Utiliser la loi normale centrée réduite
- Calculer le Z-score et les probabilités avec Excel
- Trouver des liens vers les tables de la loi normale
- Lire les tables de la loi normale
Si vous voulez construire vous-même votre courbe de Gauss avec Excel, consultez mon dossier .
La loi normale
Qu'est-ce qu'une distribution normale ?
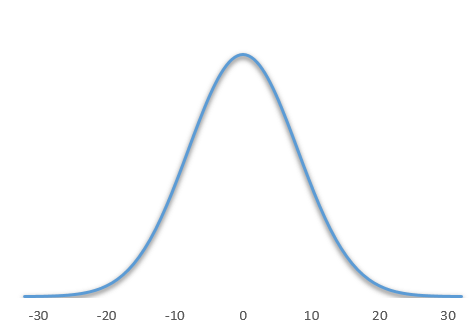
A la différence de la loi de Poisson ou de la loi binomiale qui sont des distributions de probabilité discrète, la distribution normale est une distribution de probabilité continue.
On peut parler également de distribution Gaussienne. On notera que sa représentation graphique est appelée courbe en cloche. La courbe normale a la particularité d'être symétrique.
Pourquoi la loi normale est-elle intéressante ?
La loi normale est remarquable par le fait qu'elle décrit une grande partie des phénomènes naturels. (science physique, sociale, médecine, agriculture, Business...) . Elle peut être utilisée dans un grand nombre de situations, c'est ce qui la rend si utile.
Lorsqu'un phénomène est influencé par de nombreux facteurs dont aucun n'est prépondérant les résultats des mesures de ce phénomène obéissent à une loi normale.
Quelle est la formule de la loi normale ?
La variable utilisée est continue, C'est-à-dire qu'elle peut prendre un nombre indéfini de valeurs.
Cette courbe a deux paramètres : μ et σ.
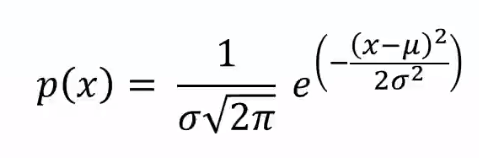
Son équation finalement très simple puisque ces 2 seuls paramètres suffisent : μ et σ. Les autres éléments de l'équation sont des constantes : Le nombre d'Euler e (2,71828) et Pi π (3.14159).
N'ayez pas peur de cette formule puisque vous n'aurez pas à l'utiliser. En effet, les outils, tel que Excel, permettent de réaliser très facilement son calcul.
Loi normale centrée réduite
Pourquoi utiliser la loi normale centrée réduite ?
Parce qu'il y a un nombre illimité de loi normale, les mathématiciens ont simplifié les choses en calculant les aires sous une loi normale spéciale de paramètres : μ=0 et de σ=1. Cette distribution est connue sous le nom de loi normale centrée réduite.
Interprétation de l'écart-type de la loi normale centrée réduite
Elle est spéciale car ses valeurs en abscisse représentent des unités d'écart-type.
Sur l'axes des abscisses on trouve des valeurs allant de -6σ à +6σ. Le centre de la courbe est positionné au-dessus de 0.
Toutes les distributions normales de moyenne 0 et d'écart-type de 1 sont appelées des distributions normales standard.
Aire sous la courbe
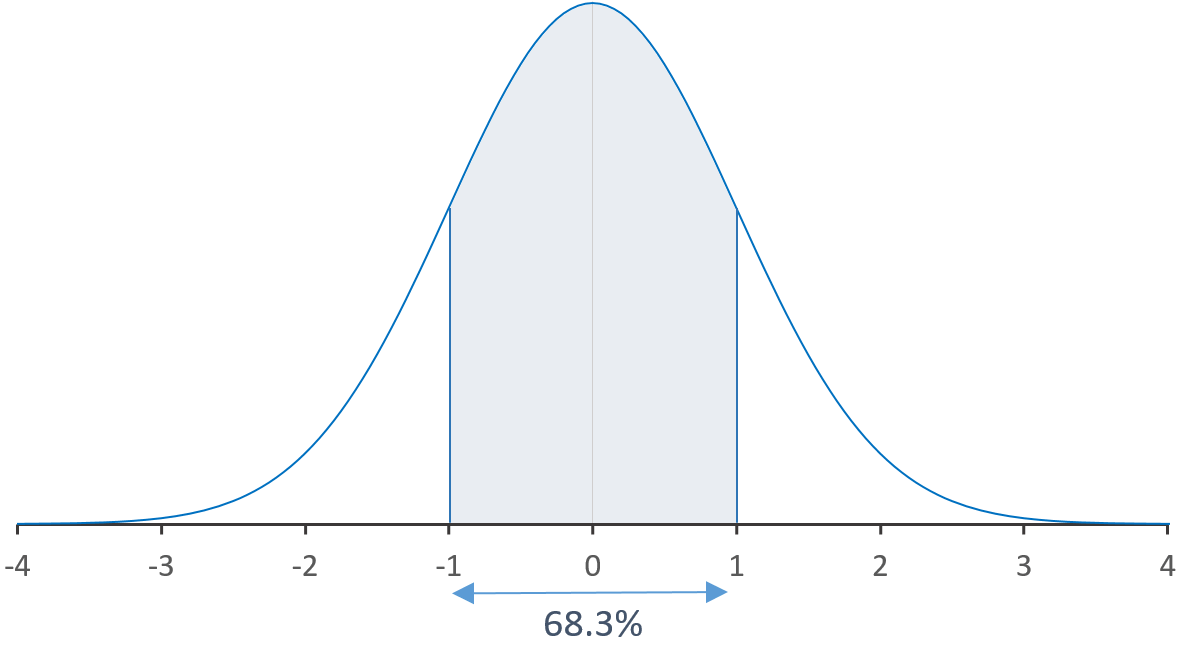
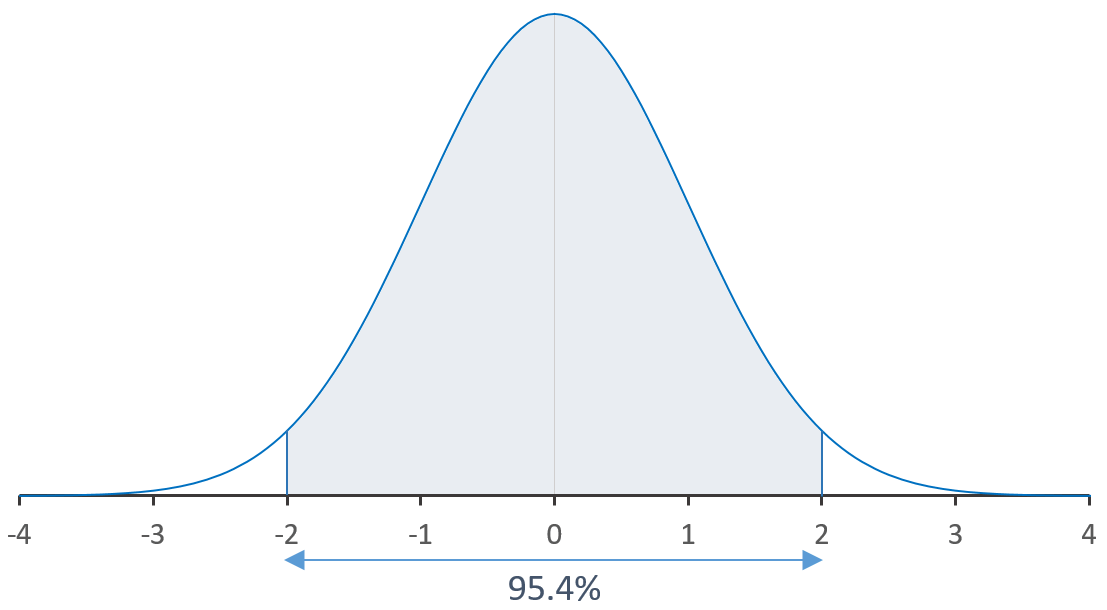
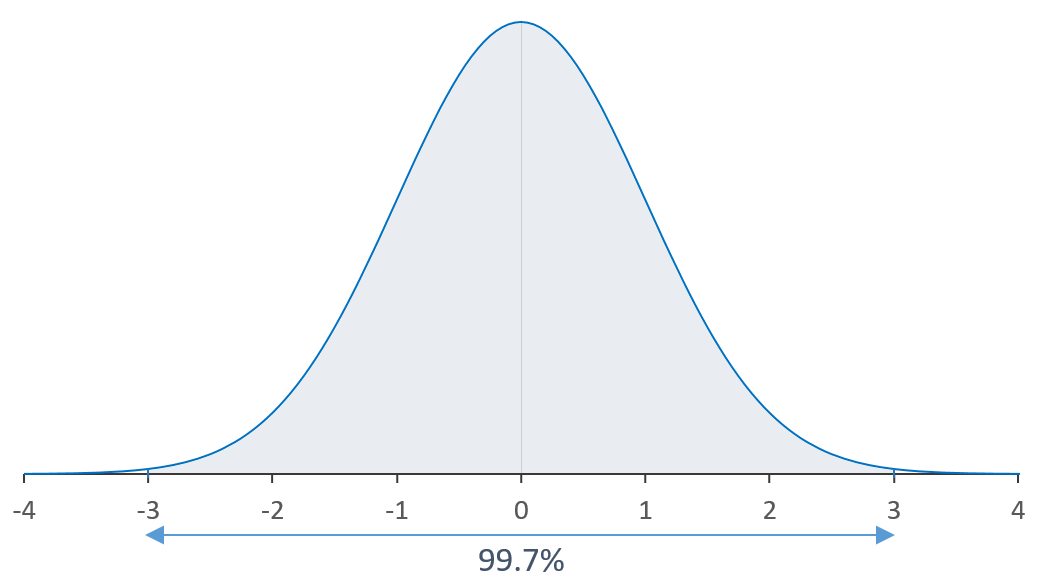
On peut ici faire les affirmations suivantes :
- entre le 0 et ±1σ vous aurez 68.3% de vos observations.
- entre le 0 et ±2σ vous aurez 95.4% de vos observations.
- entre le 0 et ±3σ vous aurez 99.7.% de vos observations.
Ces valeurs sont des valeurs remarquables. Cela nous amène de nouvelles questions :
- Comment faire pour savoir combien d'observations sont comprises entre (par exmple) 0 ± ; 1.8σ ?
Astuce Excel pour calcluer la probabilité
Il est possible d'utiliser la formule Excel suivante :
=LOI.NORMALE.STANDARD.N(Z;VRAI)-(1-LOI.NORMALE.STANDARD.N(Z;VRAI))
Par exemple, pour calculer la probabilité dans une aire comprise entre -1.8 α et +1.8 α on appliquera la formule en remplaçant Z par 1.8 :
=LOI.NORMALE.STANDARD.N(1.8;VRAI)-(1-LOI.NORMALE.STANDARD.N(1.8;VRAI))
Le résultat obtenu sera : 92.82%
Le Z-score
Pourquoi utiliser le Z-score ?
L'idée ici est de convertir les valeurs de l'unité de mesure originale en une nouvelle unité appelé le Z-score (ou cote Z). La cote Z correspond au nombre d'écarts types séparant un résultat de la moyenne.
Prenons l'exemple ci-dessous d'une distribution quelconque centré sur μ et d'écart-type σ.
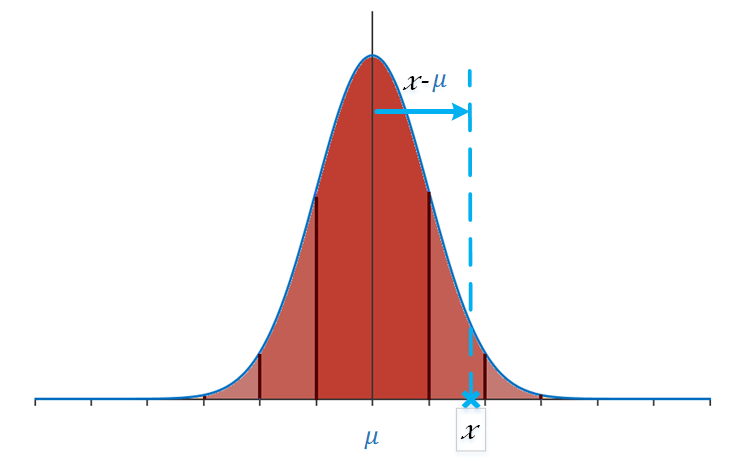
La formule est la suivante :
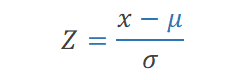
Autrement formulé, le Z score défini de combien d'écart-types la valeur recherchée est éloignée de la moyenne.
Avec ce calcul, on déplace la distribution sur "0" en retirant la valeur de la moyenne μ et on obtient un écart-type égale à "1" en divisant par l'écart-type de la population.
Le Z-score deviendra votre coordonnée. Vous n'aurez plus à soustraire μ, car la moyenne sera déjà de 0 et vous n'aurez pas à diviser par sigma σ car l'écart-type sera déjà de 1.
Utilisation de la table de la loi normale centrée réduite
Les tables sont constituées généralement d'un schéma et d'un tableau.
Les schémas
Il est important de savoir qu'il existe plusieurs types de tables de loi normale centrée réduite. La lecture de la probabilité varie d'une table à l'autre. Pour clarifier cela les tables possèdent généralement un schéma explicatif au sommet de celle-ci. Il faut donc être attentif à la zone grisée qui représente l'aire de la probabilité considérée.
Voici quelques exemples de ces schémas :
Voici quelques lien vers des tables : Lien 1 , Lien 2 .
Pour la démonstration ci-dessous, la table du Lien 1 a été utilisée. Dans ce document, vous pouvez identifier deux pages. Vous remarquez le schéma suivant sur la première page.
Remarquez un deuxième schéma en haut de la seconde page. Soyez attentif à chacun de ces 2 schémas qui indiquent précisément les zones de probabilité considérées.
Le tableau
Le Tableau a pour sa part 2 zones.
On retrouve notre variable z qui est notre donnée d'entrée. (que j'ai indiqué en marron) et notre probabilité (que j'ai indiqué en bleu).
L'unité et le premier chiffre après la virgule sont dans la première colonne. Le second chiffre se trouve sur la première ligne.
La zone centrale indique les probabilités associées. Ainsi, pour un z donné, on trouvera une probabilité spécifique.
La valeur Z commence à -3.4 et atteint zéro en bas du tableau. Ainsi cette première page concerne que les valeurs négatives de z.
Comment lire la table de la loi normale centrée réduite ?
Exemple 1: lecture de la loi normale
On lit le tableau de la façon suivante :
Pour un Z de -2.51 seul 0.6% des valeurs sont en dessous de ce seuil.
Exemple 2 : lecture de la loi normale
Prenons cette fois-ci une valeur positive de z = 1.65
Pour un Z de 1.65 seul 95.05% des valeurs sont en dessous de ce seuil.
Utilisation de la loi normale
Dans notre exemple, nous utiliserons la distribution ci-dessous :
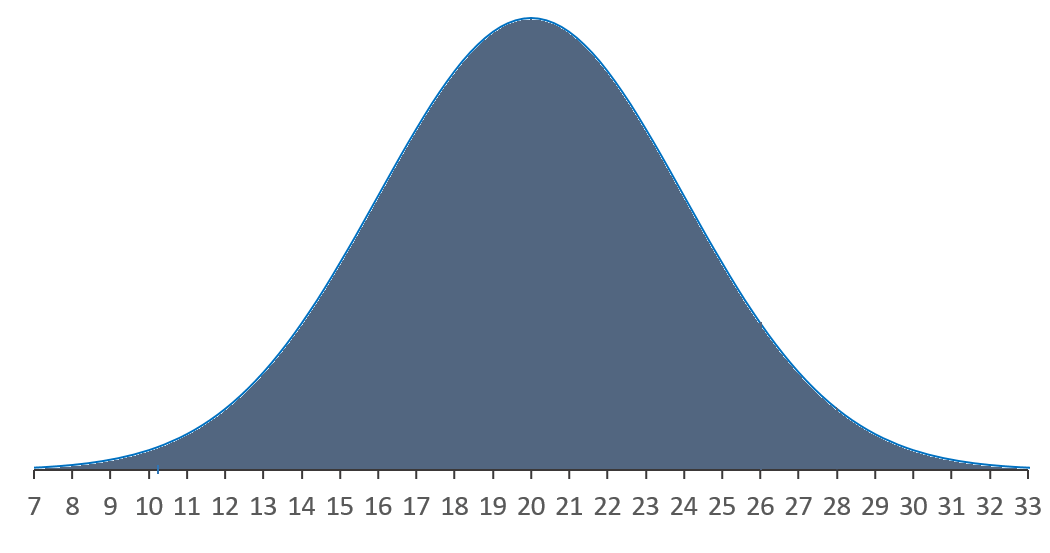
La distribution centrée sur 20 et a un écart-type égale à 2.
Rappel : Si l'on considère l'aire total sous la courbe elle est égale à 1. La probabilité est directement associée à l'aire et est également égale à 100%
Exemple de calcul de probabilité
Cas n°1
On considéra l'aire entre 2 valeurs 20 et 25 qui seront placés en abscisse.
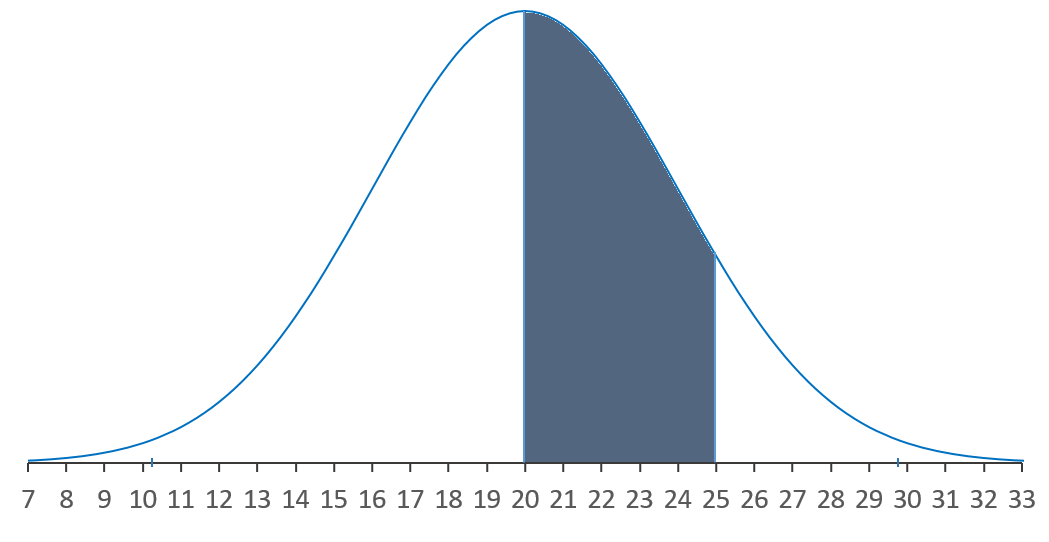
Pour déterminer la probabilité, il faut déterminer l'aire sous la courbe. Pour ce faire, on utilise la loi normale centrée réduite dont on extrapolera les résultats pour chaque distribution normale étudiée.
Z est calculé avec les paramètres suivants :
- Valeur x=25
- Moyenne μ =20
- Ecart-type σ=2
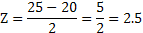
On sait grâce à ce calcul qu'il y a 2.5 σ entre 25 et 20. Si le signe de Z est positif cela signifie que l'on se situe à 2.5 σ à droite de la moyenne.
Si on lit la valeur sur la table correspondant à 2.5 sur la deuxième page, on trouvera une probabilité de 0.9938. La valeur de 0.9938 correspond à la probabilité associée à toutes les valeurs inférieures à 25. Pour obtenir la probabilité associée à l'intervalle de [20-25]. Il faut retrancher les probabilités associées à toute la partie gauche de la courbe, soit 0.5.
Ainsi la probabilité est égale à 0.9938-0.5 = 0.498.
Cas n°2
L'aire sous la courbe ne dépend pas toujours de un seul z, il peut dépendre de plusieurs z comme cela est représenté dans les intervalles étudiés suivants constitués de deux valeurs z spécifiques.
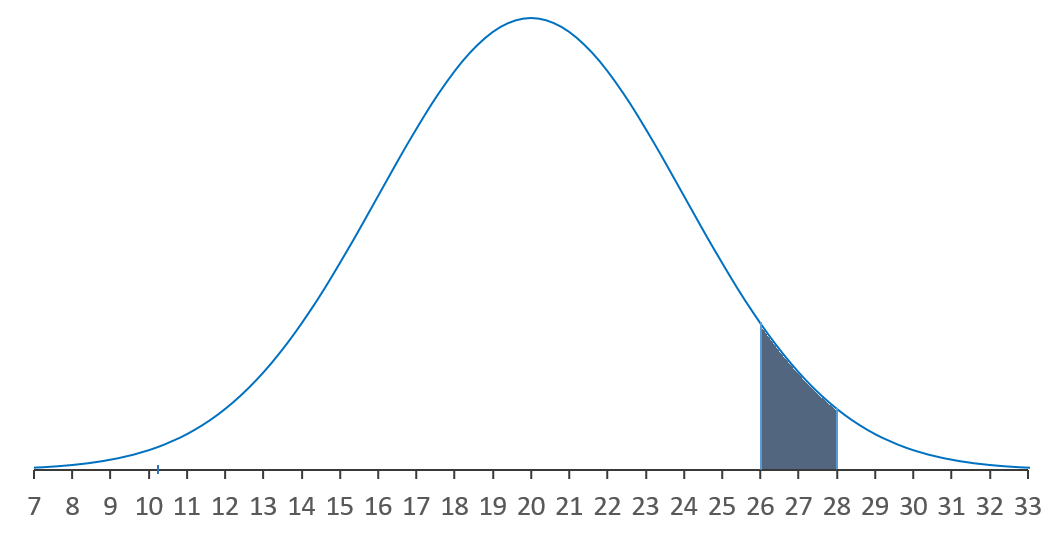
- μ=20
- σ=2
- Limite inférieure = 26
- Limite supérieure = 28
- intervalle = 2
Cas n°3

- μ=20
- σ=2
- Limite inférieure = 24
- Limite supérieure =26
- intervalle = 2
Remarques : les courbes des cas n°2 et n°3 ont les mêmes paramètres : μ et σ. L'interval est pour les deux cas est égale à 2 unités cependant l'aire sous la courbe est visiblement différente.
Afin de faciliter le calcul, vous trouverez dans le tableau de synthèse ci-dessous les calculs réalisés avec une feuille Excel. Il intègre les calculs de correspondance pour 3 situations. Les valeurs z sont caculées de la même manière pour l'exemple 1.
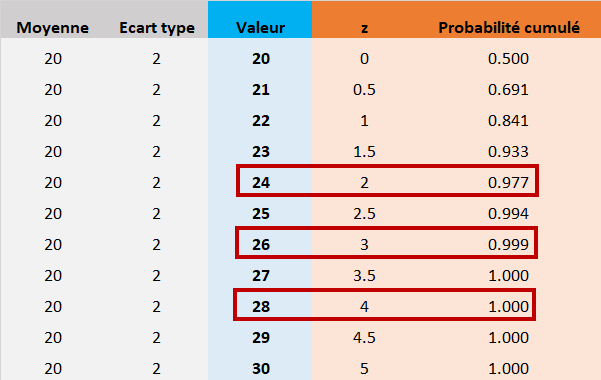
Pour obtenir la probabilité de l'aire entre les z spécifiques, on procède par soustraction des probabilités associés aux 2 valeur z.
En conséquence la probabilité du cas 2 est égale à 1-0.999 = 0.001.
En conséquence la probabilité du cas 3 est égale à 0.999-0.977 = 0.021.
Le processus est le suivant:
- Nous identifions les valeurs z de chaque limite.
- Depuis la table nous trouvons les aires pour chaque valeur z.
- En fonction de chaque situation, nous ajoutons ou soustrayons les probabilités.
Pour aller plus loin consulter également le site qui constitue une importante source de connaissance : http://onlinestatbook.com/
Exemple : Cas d'un contrôle de produits
Imaginons une entreprise produisant des meubles de cuisine. Une des cotes de hauteur est particulièrement importante pour assurer la fonction des ouvertures. Elle souhaite déterminer la qualité d'un de ses lots de production à partir d'un échantillon.
L'échantillon aura les paramètres suivants- x =50.41
- s=0.1
- Cible et tolérance: 50.5 ±0.2
- Limite inférieure = 50.3
- Limite supérieure =50.7
- intervalle = 0.4
Les valeurs de z sont calculées de la façon suivante :
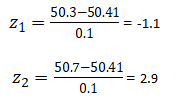
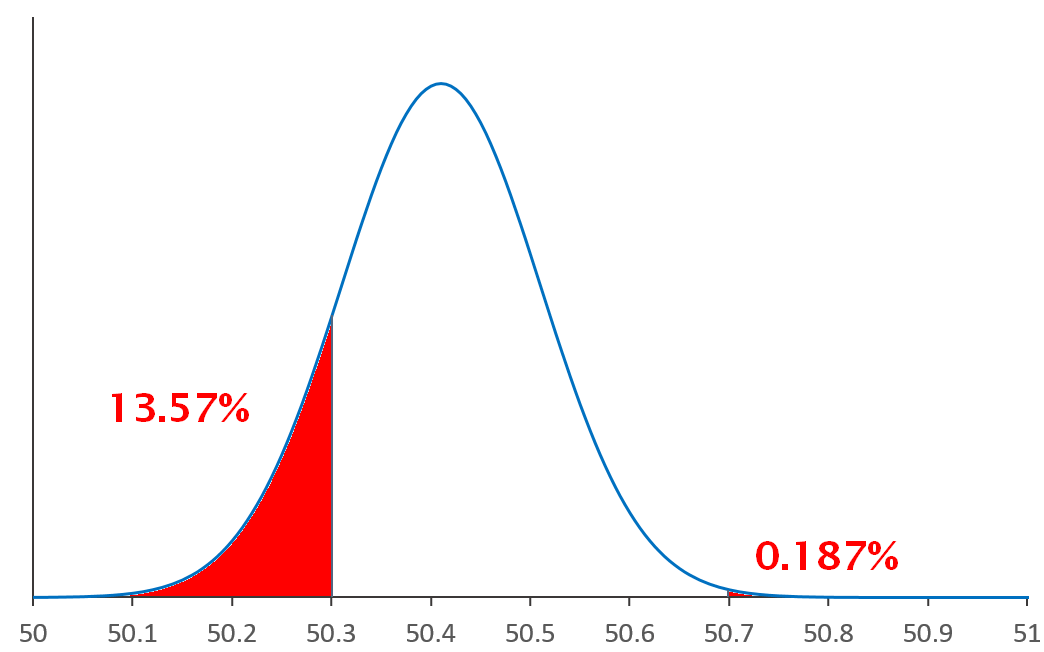
A l'aide de la table nous obtenons la probabilité P1=13.57% par une lecture directe.
La probabilité P2 se fait en 2 temps. Tout d'abord en lisant la valeur correspondante au z de 2.9 : 0.9981 puis en soustrayant cette valeur à 1 :
1-0.9981 = 0.00187 soit 0.187%
La proportion de pièces non-conformes est de 13.57%+0.187% = 13.757%
Autres dossiers sur l'analyse de données sur commentprogresser.com
Découvrez nos micro-formations et conseils en:
- Utilisation des outils qualité
- Le contrôle qualité
- Techniques de résolution de problèmes
- Le tableaux de bord qualité
- ... et bien plus encore!
Formations sur mesure adaptées à VOS besoins, disponibles rapidement.
📩Écrivez-nous à: commentprogresser@gmail.com
Nicolas DEROBERT


